Question

Find the solution(s) to the equation Sine (StartFraction x Over 2 EndFraction) + cosine x minus 1 = 0 on the interval 0 ≤ x 2π.

Check all that apply

Answer 1

0

StartFraction pi Over 3 EndFraction

StartFraction 5 pi Over 3 EndFraction

Explanation:

A,B,E

Answer 2

All apply values are:

0 ⇒ A

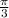`(\pi )/(3)` ⇒ B

`(5\pi )/(3)` ⇒ E

Explanation:

∵ 0 ≤ x ≤ 2π is the domain for angle x

∴ 0 ≤
`(x)/(2)` ≤ π is the domain of angle

∵ sin(
`(x)/(2)`) + cos(x) - 1 = 0

→ To solve the equation we should use the rule of cosine double angle

∵ cos(x) = 1 - 2 sin²(
`(x)/(2)`)

→ Substitute it in the equation above

∴ sin(
`(x)/(2)`) + (1 - 2 sin²(
`(x)/(2)`) = 0

∴ sin(
`(x)/(2)`) + 1 - 2 sin²(
`(x)/(2)`) = 0

→ Add the like terms

∴ sin(
`(x)/(2)`) + (1 - 1) - 2 sin²(
`(x)/(2)`) = 0

∴ sin(
`(x)/(2)`) - 2 sin²(
`(x)/(2)`) = 0

→ Take sin(
`(x)/(2)`) as a common factor

∴ sin(
`(x)/(2)`) [1 - 2sin(
`(x)/(2)`)] = 0

→ Equate each factor by 0

∵ sin(
`(x)/(2)`) = 0

→ The value of sine equal zero on the x-axis

∴
`(x)/(2)` = 0, π, 2π

∵ The domain of
`(x)/(2)` is 0 ≤ (
`(x)/(2)`) ≤ π

∴
`(x)/(2)` = 0 and π ⇒ 2π refused because ∉ the domain

→ Multiply both sides by 2 to find x

∴ x = 0 and 2π

∵ 1 - 2sin(
`(x)/(2)`) = 0

→ Subtract 1 from both sides

∴ - 2sin(
`(x)/(2)`) = -1

→ Divide both sides by -2

∴ sin(
`(x)/(2)`) =
`(1)/(2)`

→ The sine is positive in the 1st and 2nd quadrants

∴ (
`(x)/(2)`) lies on the 1st OR 2nd quadrants

∵ (
`(x)/(2)`) =
`sin^(-1)((1)/(2))`

∴ (
`(x)/(2)`) =
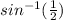
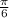`(\pi )/(6)` ⇒ 1st quadrant

→ Multiply both sides by 2

∴ x =
`(\pi )/(3)`

∵ (
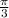
`(x)/(2)`) = π -
`(\pi )/(6)` =
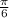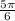`(5\pi )/(6)` ⇒ 2nd quadrant

→ Multiply both sides by 2

∴ x =
`(5\pi )/(3)`

∴ The values of x are 0,
`(\pi )/(3)`,
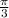`(5\pi )/(3)`, 2π

All apply values are:

0 ⇒ A

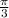`(\pi )/(3)` ⇒ B

`(5\pi )/(3)` ⇒ E