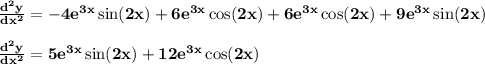Question

Please help me do this question​

Answer 1

`\tt{ \frac{ {d}^(2) y}{d {x}^(2) } = 5 {e}^(3x) \sin(2x) + 12 {e}^(3x) \cos(2x)}`

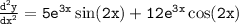
Explanation:

⠀

⠀

⠀⠀⠀⠀▩ Question

`y = {e}^(3x) \sin(2x) \\ { \sf{To \: find}} \: \frac{ {d}^(2)y }{d {x}^(2) }`

⠀

⠀

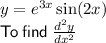
⠀⠀⠀⠀■ Solution

⠀

• First finding dy/dx

⠀

`\sf using \: (d)/(dx) uv = u (d)/(dx) v + v (d)/(dx) u \: formula`

⠀

⠀

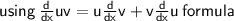
• Taking derivative of sin2x and e^3x

⠀

`\bold{ (dy)/(dx) = {e}^(3x) (d)/(dx) \sin(2x) + \sin(2x) (d)/(dx) {e}^(3x) } \\ \\ \bold{ (dy)/(dx) = {e}^(3x) \cos(2x) (d)/(dx) 2x + \sin(2x) {e}^(3x) (d)/(dx) 3x}`

⠀

⠀

• Multiplying

⠀

`\bold{ (dy)/(dx) = {e}^(3x) * 2 \cos(2x) + \sin(3x) * 3 {e}^(3x) }`

⠀

⠀

• Value of dy/dx

⠀

`\bold{ (dy)/(dx) = 2 {e}^(3x) \cos(2x) + 3 {e}^(3x) \sin(2x) }`

⠀

⠀

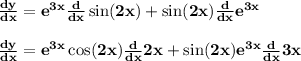
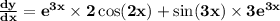
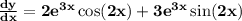
• Now taking derivative again using same formula as mention in first part, so that to find d²y/dx².

⠀

⠀

⠀⠀● First solving 2e^3x cos(2x)

⠀

`\bold{ 2( {e}^(3x) (d)/(dx) \cos(2x) + \cos(2x) (d)/(dx) {e}^(3x)) }`

⠀

⠀

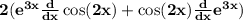
• Taking derivative of cos2x and e^3x

⠀

`\bold{2( {e}^(3x) - \sin(2x) (d)/(dx) 2x + \cos(2x) {e}^(3x) (d)/(dx) 3x)} \\ \\ \bold{ - 4 {e}^(3x) \sin(2x) + 6 {e}^(3x) \cos(2x) }`

⠀

⠀

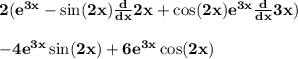
⠀⠀● Now solving 3e^3x sin(2x)

⠀

`\bold{ 3( {e}^(3x) (d)/(dx) \sin(2x) + \sin(2x) (d)/(dx) {e}^(3x) )}`

⠀

⠀

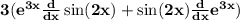
• Now taking derivative of sin 2x and e^3x

⠀

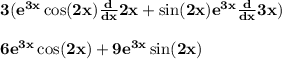
`\bold{ 3( {e}^(3x) \cos(2x) (d)/(dx) 2x + \sin(2x) {e}^(3x) (d)/(dx) 3x)} \\ \\ \bold{ 6 {e}^(3x) \cos(2x) + 9 {e}^(3x) \sin(2x) }`

⠀

⠀

• Adding both solution

⠀

`\bold{ \frac{ {d}^(2)y }{d {x}^(2) } = - 4 {e}^(3x) \sin(2x) + 6 {e}^(3x) \cos(2x) + 6 {e}^(3x) \cos(2x) + 9 {e}^(3x) \sin(2x) } \\ \\ \bold{ \frac{ {d}^(2) y}{d {x}^(2) } = 5 {e}^(3x) \sin(2x) + 12 {e}^(3x) \cos(2x) }`

Answer 2

`(d^2y)/(dx^2) = 5e^(3x) \sin (2x)+12e^(3x) \cos (2x)`

Explanation:

`\large \boxed{\begin{minipage}{5 cm}\textsf{\underline{Product Rule}}\\\\$ \textsf{When } \:y=uv\\\\(dy)/(dx)=u(dv)/(dx)+v (du)/(dx)$\\\end{minipage}}`

Given:

`y=e^(3x) \sin(2x)`

First Derivative

`\textsf{let } u=e^(3x) \implies (du)/(dx)=3e^(3x)`

`\textsf{let } v= \sin(2x) \implies (dv)/(dx)=2 \cos (2x)`

Using the Product Rule:

`\begin{aligned}(dy)/(dx) & =e^(3x)\cdot 2 \cos (2x) + \sin (2x) \cdot 3e^(3x)\\& = 2e^(3x) \cos (2x) + 3e^(3x) \sin (2x)\\& = e^(3x)(2 \cos (2x) + 3 \sin (2x))\end{aligned}`

Second Derivative

`\textsf{let } u=e^(3x) \implies (du)/(dx)=3e^(3x)`

`\textsf{let } v= 2 \cos (2x)+3 \sin (2x) \implies (dv)/(dx)=-4 \sin (2x) +6 \cos (2x)`

Using the Product Rule:

`\begin{aligned}(d^2y)/(dx^2) & =e^(3x)(-4 \sin (2x) +6 \cos (2x)) +3e^(3x) (2 \cos (2x)+3 \sin (2x))\\& = e^(3x)[-4 \sin (2x) +6 \cos (2x)+6 \cos (2x)+9 \sin (2x)]\\& = e^(3x)[5 \sin (2x) +12 \cos (2x)]\\& = 5e^(3x) \sin (2x)+12e^(3x) \cos (2x)\end{aligned}`