Question

Find the exact value of cos(a + b), given sin a = 2/5 for a in Quadrant || and cos B = 1/3 for b in Quadrant IV.

Answer 1

Answer: D

Explanation:

Edge 2021

Answer 2

Option (4)

Explanation:

cos(a + b) = cos(a)cos(b) - sin(a)sin(b) [Identity]

Since, sin(a) =
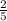`(2)/(5)` for a in quadrant II

Therefore, cos(a) =
`\sqrt{1-\text{sin}^2(a)}=\sqrt{1-((2)/(5))^2}`

cos(a) =
`(√(21))/(5)`

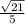
But cosine of a is negative quadrant II

Therefore, cos(a) = -
`(√(21))/(5)`

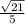
And cos(b) =
`(1)/(3)` for b in quadrant IV

Therefore, sin(b) =
`\sqrt{1-\text{cos}^(2)b}`

=
`\sqrt{1-((1)/(3))^2}`

=
`(2√(2))/(3)`

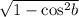
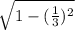
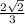
But sine of an angle is negative in quadrant IV,

Therefore, sin(b) =
`-(2√(2))/(3)`

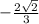
Now substituting these values in the identity,

cos(a + b) =
`(-(√(21))/(5))((1)/(3))-((2)/(5))(-(2√(2))/(3))`

=
`-(√(21))/(15)+(4√(2))/(15)`

=
`(4√(2)-√(21))/(15)`

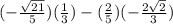
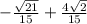
Therefore, Option (4) will be the answer.