Answer:
Option (4)
Explanation:
cos(a + b) = cos(a)cos(b) - sin(a)sin(b) [Identity]
Since, sin(a) =
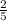 for a in quadrant II
for a in quadrant II
Therefore, cos(a) =
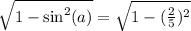
cos(a) =
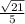
But cosine of a is negative quadrant II
Therefore, cos(a) = -
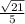
And cos(b) =
 for b in quadrant IV
for b in quadrant IV
Therefore, sin(b) =
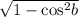
=
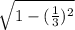
=
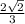
But sine of an angle is negative in quadrant IV,
Therefore, sin(b) =
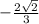
Now substituting these values in the identity,
cos(a + b) =
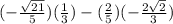
=
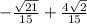
=
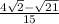
Therefore, Option (4) will be the answer.