Answer:
The total force on the charge placed in the middle will be zero (0).
Step-by-step explanation:
The force on the charge in the middle of a square due to one of the charges placed at the square corner is given by:
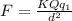
Where:
Q: is the charge in the middle = 1 nC
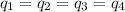 are the charge placed at the 4 square corners = -2 nC
are the charge placed at the 4 square corners = -2 nC
The distance between the charge Q and q₁, q₂, q₃, and q₄ is:
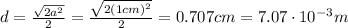
Now, the magnitude of the force is:
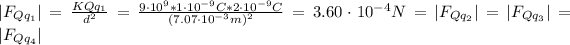
Since the magnitude of the force on the charge placed in the middle of the square is the same due to the 4 charges placed in the square corners (because the charge of q₁, q₂, q₃, and q₄ charges is the same) and due to the geometry, the vectorial sum of the total force on the charge placed in the middle will be zero (0).
Therefore, the total force on the charge placed in the middle will be zero (0).
I hope it helps you!