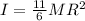Answer: I =
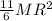
Step-by-step explanation: Moment of Inertia (I) is the opposition on a rotating body. Generally, is calculated by
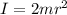
A bycicle wheel is composed of numerous parts and each part has its own moment of inertia.
Moment of inertia for this 5-spoke bike wheel will be:
Inertia of ring:

For the 5-spoke wheel:
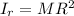
Inertia of spokes:
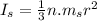
where
n is the number of spokes
For the 5-spoke wheel, half of the total mass is the spokes, then:
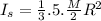
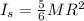
Inertia of the wheel is the sum of both inertia:
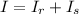
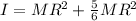
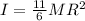
The moment of inertia of the 5-spoke bike wheel is