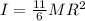Question

An expensive carbon weave 5-spoke bike wheel has total mass M and radius R. If half the mass of the wheel is in the spokes, what is this wheel's moment of inertia?

Answer 1

Answer: I =
`(11)/(6)MR^(2)`

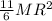
Step-by-step explanation: Moment of Inertia (I) is the opposition on a rotating body. Generally, is calculated by
`I=2mr^(2)`

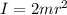
A bycicle wheel is composed of numerous parts and each part has its own moment of inertia.

Moment of inertia for this 5-spoke bike wheel will be:

Inertia of ring:
`I_(r)=m_(r)r^(2)`

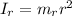
For the 5-spoke wheel:

`I_(r)=MR^(2)`

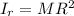
Inertia of spokes:
`I_(s)=(1)/(3)n.m_(s)r^(2)`

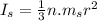
where

n is the number of spokes

For the 5-spoke wheel, half of the total mass is the spokes, then:

`I_(s)=(1)/(3).5. (M)/(2)R^(2)`

`I_(s)=(5)/(6)MR^(2)`

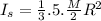
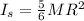
Inertia of the wheel is the sum of both inertia:

`I=I_(r)+I_(s)`

`I=MR^(2)+(5)/(6)MR^(2)`

`I=(11)/(6)MR^(2)`

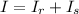
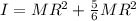
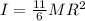
The moment of inertia of the 5-spoke bike wheel is
`I=(11)/(6)MR^(2)`