Question

NEED ASAP

For a sewing project, Tanya cut isosceles triangles from a striped piece of material where the stripes are parallel. The vertex angle of the isosceles triangle is 50° and overline BC is parallel to the base.




What is the measure of BCE as shown in the diagram? Show your work and
explain your reasoning.

Answer 1

∠BCE is 115°

Explanation:

The given parameters are;

The shape Tanya cut from the striped piece = Isosceles triangles

The measure of the vertex angle of the isosceles triangle = 50°

The segment
`\overline {BC}` is parallel to the base
`\overline {FG}`

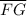
Therefore, we have;

∠GAF + ∠AGF + ∠AFG = 180°; Sum of the interior angles of a triangle

∴ ∠AGF + ∠AFG = 180° - ∠GAF = 180° - 50° = 130°

∠AGF = ∠AFG; Base angles of an isosceles triangle

∴ ∠AGF + ∠AFG = ∠AGF + ∠AGF = 2 × ∠AGF = 130°

∠AGF = 130°/2 = 65°

∠AGF = 65°

∠AGF ≅ ∠ACB, corresponding angles of two parallel lines,
`\overline {BC}` and
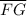`\overline {FG}` cut by a transversal
`\overline {AG}`

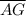
∠AGF = ∠ACB = 65°, definition of congruency

∠ACB + ∠BCE = 180° Sum of angles on a (straight) line

∠BCE = 180° - ∠ACB = 180° - 65° = 115°

∠BCE = 115°