Answer:
The heater resistance is 2.167 ohms.
Step-by-step explanation:
According to the First Law of Thermodynamics, electric work becomes heat transfer rate. From Ohm's Law and definition of efficiency we get that output heat rate (
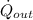 ), measured in watts, is represented by:
), measured in watts, is represented by:
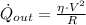 (Eq. 1)
(Eq. 1)
Where:
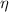 - Heating efficiency, dimensionless.
- Heating efficiency, dimensionless.
 - Power supply voltage, measured in volts.
- Power supply voltage, measured in volts.
 - Heater resistance, measured in ohms.
- Heater resistance, measured in ohms.
Now we clear the heater resistance:
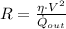
If we know that
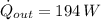 ,
,
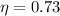 and
and
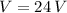 , then the heater resistance is:
, then the heater resistance is:

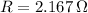
The heater resistance is 2.167 ohms.