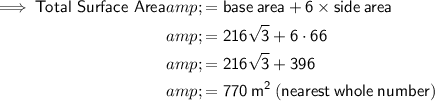Answer:
770 m²
Explanation:
The surface area of a regular pyramid comprises the area of the base (regular polygon) and the area of each of the slanted sides (triangles).
Apothem: The line segment from the center of the regular polygon to the midpoint of one of its sides.
Area of the base
The base of the prism is a regular polygon with 6 sides (hexagon).

where:
- n = number of sides
- s = side length
- a = apothem
Given:
Substitute the given values into the formula:
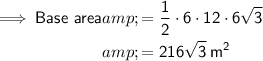
Area of one side
The sides of the regular pyramid are congruent triangles.
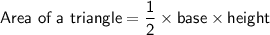
Given:
Substitute the given values into the formula:
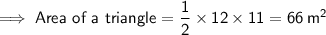
Total Surface Area