Answer:
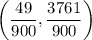 or approximately (0.544, 4.179)
or approximately (0.544, 4.179)
Explanation:
A function and its tangent lines intersect when their slopes are the same. Find the x-coordinate when the slope of f(x) is equal to 8/7 by taking the derivative of f(x):
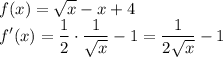
Set
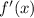 equal to 8/7 and solve for x:
equal to 8/7 and solve for x:
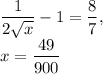
Therefore,
 will intersect at a point of tangency with a line of slope 8/7 at x=49/900. Plug in x=49/900 into
will intersect at a point of tangency with a line of slope 8/7 at x=49/900. Plug in x=49/900 into
 to get the y-coordinate:
to get the y-coordinate:
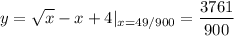
⇒Answer: (49/900, 3761/900) or approximately (0.544, 4.179)