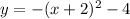Question

(-2,-4)

Oy=(x + 2)² +4
Oy=(x - 2)²-4
Oy=-(x - 2)²-4
Oy=-(x + 2)² - 4

Answer 1

y = -(x + 2)² - 4

Explanation:

Vertex form of an equation :

y = a(x - h)² + k

• Vertex = (h, k)

Substituting the coordinates of the vertex in the equation :

y = (x -(-2))² + (-4)

y = (x + 2)² - 4

y = -(x + 2)² - 4 (as the graph opens downwards)

Answer 2

`\textsf{D)} \quad y=-(x+2)^2-4`

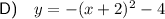
Explanation:

Vertex form of a quadratic equation:

`y=a(x-h)^2+k`

where:

• 
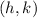  `(h, k)` is the vertex
• 
  `a` is some constant
  If
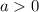  `a > 0`, the parabola opens upwards
  If
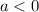  `a < 0`, the parabola opens downwards

From inspection of the graph, the vertex (turning point) is (-2, -4).

Substituting the vertex into the equation:

`\implies y=a(x-(-2))^2+(-4)`

`\implies y=a(x+2)^2-4`

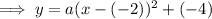
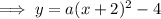
As the parabola opens downwards,
`a < 0`:

`\implies y=-a(x+2)^2-4`

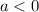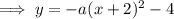
The curve intercepts the y-axis at (0, -8).

Inputting this into the equation and solving for
`a`:

`\implies -8=-a(0+2)^2-4`

`\implies -4=-4a`

`\implies a=1`

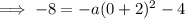
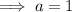
Therefore, the equation of the graph is:

`y=-(x+2)^2-4`