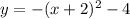Answer:
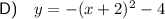
Explanation:
Vertex form of a quadratic equation:
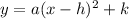
where:
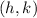 is the vertex
is the vertex
 is some constant
is some constant
If
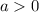 , the parabola opens upwards
, the parabola opens upwards
If
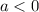 , the parabola opens downwards
, the parabola opens downwards
From inspection of the graph, the vertex (turning point) is (-2, -4).
Substituting the vertex into the equation:
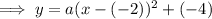
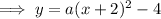
As the parabola opens downwards,
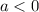 :
:
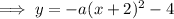
The curve intercepts the y-axis at (0, -8).
Inputting this into the equation and solving for
 :
:
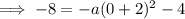
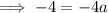
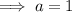
Therefore, the equation of the graph is: