Please answer this question

Question

asked May 3, 2023 218k views

1 Answer

BimoZX · Answer 1 · 2023-05-08T08:39:37+0000

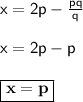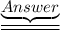
$\bold{\underline{\underline{\underbrace{Answer}}}}$

x = p and y = -q

Explanation:

The value of x and y

px + qy = p² - q²(equation 1)

qx - py = 2py

{Taking equation 2}

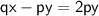
$\sf qx - py = 2py$

{Taking py on RHS}

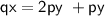
$\sf qx = 2py \ + py$

{Dividing both sides by q

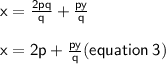
$\sf x = (2pq)/(q) + (py)/(q) \\ \\ \sf x = 2p + (py)/(q) (equation \: 3)$

{Now substituting the value of equation 3 in equation 1}

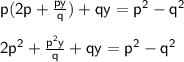
$\sf p(2p + (py)/(q) ) + qy = {p}^(2) - {q}^(2) \\ \\ \sf 2 {p}^(2) + \frac{ {p}^(2)y }{q} + qy = {p}^(2) - {q}^(2)$

{Taking 2p² on RHS and taking LCM on LHS}

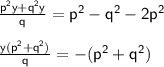
$\sf \frac{ {p}^(2)y + {q}^(2) y }{q} = {p}^(2) - {q}^(2) - 2 {p}^(2) \\ \\ \sf \frac{y( {p}^(2) + {q}^(2) ) }{q} = - ( {p}^(2) + {q}^(2) )$

{Dividing (p² + q²) both sides}

$\sf (y)/(q) = - 1 \\ \\ \red{ \boxed {\bold{y = - q}} }$

{Now using value of y in equation 3}

$\sf x = 2p - (pq)/(q) \\ \\ \sf x = 2p - p \\ \\ \red{ \boxed{ \bold{ x = p}}}$