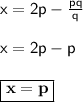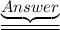
x = p and y = -q
Explanation:
The value of x and y
px + qy = p² - q²(equation 1)
qx - py = 2py
{Taking equation 2}
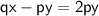
{Taking py on RHS}
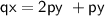
{Dividing both sides by q
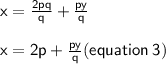
{Now substituting the value of equation 3 in equation 1}
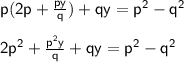
{Taking 2p² on RHS and taking LCM on LHS}
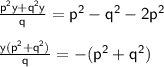
{Dividing (p² + q²) both sides}
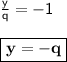
{Now using value of y in equation 3}