Question

Consider the quadratic function shown in the table below. x y 0 0 1 3 2 12 3 27 Which exponential function grows at a faster rate than the quadratic function for 0< x < 3?

Answer 1

So values are

• (0,0)
• (1,3)
• (2,12)
• (3,27)

The rule is

• 3/1=3
• 12/2=6
• 27/3=9

Explicit formula

• x(3x) where x is set of integers

Equation here is

• y=3x²

Answer 2

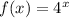`f(x)=4^x` grows at a faster rate than the given quadratic function.

Explanation:

Given table:

`\large \begin{array} c \cline{1-2} x & y \\\cline{1-2} 0 & 0 \\\cline{1-2} 1 & 3 \\\cline{1-2} 2 & 12 \\\cline{1-2} 3 & 27 \\\cline{1-2}\end{array}`

First Differences in y-values:

`0 \overset{+3}{\longrightarrow} 3 \overset{+9}{\longrightarrow} 12 \overset{+15}{\longrightarrow} 27`

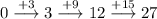
Second Differences in y-values:

`3 \overset{+6}{\longrightarrow} 9 \overset{+6}{\longrightarrow} 15`

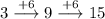
As the second differences are the same, the function is quadratic.

The coefficient of
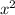`x^2` is always half of the second difference.

Therefore, the quadratic function is:

`f(x)=3x^2`

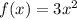
The average rate of change of function f(x) over the interval a ≤ x ≤ b is given by:

`(f(b)-f(a))/(b-a)`

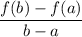
Therefore, the average rate of change for
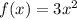`f(x)=3x^2` over the interval
0 ≤ x ≤ 3 is:

`\textsf{Average rate of change}=(f(3)-f(0))/(3-0)=(27-0)/(3-0)=9`

An exponential function that grows at a faster rate than
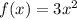`f(x)=3x^2` over the interval 0 ≤ x ≤ 3 is
`f(x)=4^x`

`\large \begin{array} c \cline{1-5} x & 0 & 1 & 2 & 3 \\\cline{1-5} f(x)=4^x & 1 & 4 & 16 & 64\\\cline{1-5} \end{array}`

`\textsf{Average rate of change}=(f(3)-f(0))/(3-0)=(64-1)/(3-0)=21`

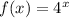
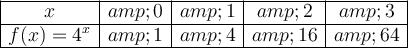
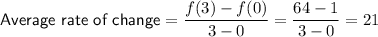
As 21 > 9,
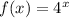`f(x)=4^x` grows at a faster rate than
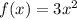`f(x)=3x^2` over the interval 0 ≤ x ≤ 3.