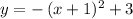Question

Help!!! Write the equation of the parabola in vertex from

Answer 1

`y=-\,(x+1)^2+3`

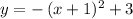
Explanation:

Notice that the vertex of the parabola is at (-1, 3), so we can start the expression of the quadratic in vertex form as:

`y=a\,(x--1)^2+3\\y = a\,(x+1)^2+3`

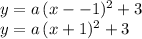
we can now find the coefficient "a" by using another point the parabola goes through, like for example (0,2):

`y = a\,(x+1)^2+3\\2=a\,(0+1)^2+3\\2=a+3\\a=2-3\\a=-1`

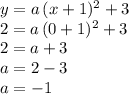
So the final expression for the parabola in vertex form is:

`y=-\,(x+1)^2+3`