Question

Find the value of the expression:
a
0.25^15·4^15

Answer 1

The value of the expression that we have is 1.

The multiplication law of indices is a fundamental rule in algebra that simplifies expressions involving exponentiation. When you multiply two terms with the same base, you can streamline the expression by adding their respective exponents.

The law indicates that when you multiply two terms with the same base, you add their exponents to simplify the expression.

The law has broad applications, proving especially useful in algebraic manipulations, simplifying expressions involving variables and constants.

We have that;

`0.25^(15).4^(15)`

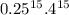
So;

`0.25^(15) * 4^(15)`

=
`(2^(-2))^(15) * (2^2)^{15`

=
`2^(-30) * 2^{30`

=
`2^{-30 + 30`

=
`2^0`

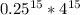
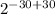
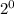
= 1