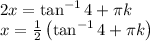Answer:
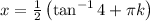 , where k is any integer
, where k is any integer
Explanation:
Let's start by getting all the trig functions on one side and all the constants on the other. We can do this by dividing both sides by
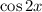 :
:

This ratio looks familiar! It just so happens that the tangent function is defined as the ratio of sine to cosine. In our case:
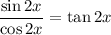
Substituting this back into our equation, we have
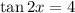 . We can unwrap the 2x by applying the inverse tangent function to both sides, giving us
. We can unwrap the 2x by applying the inverse tangent function to both sides, giving us
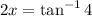 . Note, this specific solution only accounts for values of 2x between 0 and 2π radians. To make it general, we can add the term πk to the end of the right side, where k is any integer. We use π as a coefficient because the tangent function has a period of π radians, and it repeats its values every period.
. Note, this specific solution only accounts for values of 2x between 0 and 2π radians. To make it general, we can add the term πk to the end of the right side, where k is any integer. We use π as a coefficient because the tangent function has a period of π radians, and it repeats its values every period.
Finally, we divide both sides of the equation by 2 to isolate x, giving us