Question

Point P′(5, −4) is the image of point P(2, 3) under a translation. What is the image of (6, −2) under the same translation?

A. (7, −1)
B. (13, −3)
C. (9, −9)
D. (3, 5)

Answer 1

Answer: (9, −9)c

Explanation:

Answer 2

C. (9, -9)

Explanation:

From Linear Algebra, we understand translations as the following vector sum:

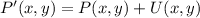`P'(x,y) = P(x,y) +U(x, y)` (Eq. 1)

Where:

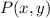`P(x,y)` - Original vector with respect to origin, dimensionless.

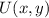`U(x,y)` - Translation vector, dimensionless.

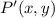`P'(x,y)` - Translated vector with respect to origin, dimensionless.

If we know that
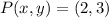`P(x,y) = (2,3)` and
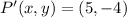`P'(x,y) =(5,-4)`, then the translation vector is:

`U(x,y) = P'(x,y)-P(x,y)`

`U(x,y) = (5,-4)-(2,3)`

`U(x,y) =(5-2,-4-3)`

`U(x,y) =(3,-7)`

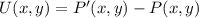
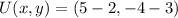
Now, if we assume that
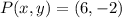`P(x,y) = (6,-2)`, then the translated vector is:

`P'(x,y) =(6,-2) +(3,-7)`

`P'(x,y) =(9,-9)`

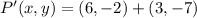
Hence, the correct answer is C.