Question

Help!!!! due now ( right answer's only)

Answer 1

hey we were talking in the comment section with someone else 16 min ago and that chat maxed out so he made another one and wants you to come back. Just letting you know.

Explanation:

Answer 2

Minimum, Vertex(1,-7) and sorry what do you mean by aos? i dont get that please type in the comments I'll answer that too. Hope you understand the rest

Explanation:

The vertex of a parabola means the stationary point/turning point which is denoted by the following:

`x=(-b)/(2a) \\`

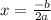
and for y we just simply put the value of x that we get into the equation so lets get started

The equation
`y=x^2-2x-6` is a quadratic equation

and if we compare it by the standard form
`y=ax^2+bx+c` we get the following values

a=1 , b=-2 , c=-6

and now for the vertex

`x=(-b)/(2a)`

`x=(-(-2))/(2(1)) \\x=(2)/(2) \\x=1`

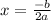
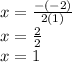
and now for y

`y=x^2-2x-6\\y=(1)^2-2(1)-6\\y=1-2-6\\y=-7`

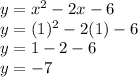
so the vertex is (1,-7)

and the graph is minimum not maximum because the value of a is greater than 0 if the value of a>0 then the graph is minimum and if the value of a<0 meaning a is negative the graph is maximum and here in the equation a=1 which means a>0 then our graph is minimum.