It looks like the given function is
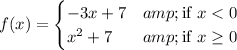
The two pieces of f(x) are continuous since they are polynomials, so we only need to worry about the point at which they meet, x = 0. f(x) is continuous there if
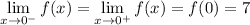
To the left of x = 0, we have x < 0, so f(x) = -3x + 7 :
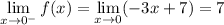
To the right of x = 0, we have x > 0 and f(x) = x² + 7 :
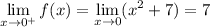
So f(x) is continuous at x = 0, and hence continuous for all real numbers.