Question

The capacities (in ampere-hours) were measured for a sample of 120 batteries. The average was 178 and the standard deviation was 12. Find a 95% lower confidence bound for the mean capacity of this type of battery. Round the answer to two decimal places. The lower confidence bound is .

Answer 1

Answer: A 95% lower confidence bound for the mean capacity of this type of battery = 175.85

Explanation:

Given: The capacities were measured for a sample : n= 120 batteries.

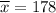`\overline{x}=178` and
`\sigma=12`

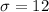
lower confidence bound=
`\overline{x}-z^c*(\sigma)/(√(n))`

Critical z value for 9%% confidence = 1.96

So, a 95% lower confidence bound for the mean capacity of this type of battery will be :

`178-(1.96)(12)/(√(120))\\\\=178-(1.96)(1.0954451)\\\\=(1.96)(1.0954451)\approx175.85`

Hence, a 95% lower confidence bound for the mean capacity of this type of battery = 175.85