Question

Please help! awarding 80 pts :DD

Answer 1

Check the picture below.

we know that the line AT is a tangent to the circle, so any radius line coming from the center of the circle will meet AT at the point of tangency, which is always a right-angle.

So we can say that line AT is perpendicular to line PA, as you see in the picture, line PA has a slope of 15/8, keeping in mind that perpendicular lines have negative reciprocal slopes then

`\stackrel{\textit{perpendicular lines have \underline{negative reciprocal} slopes}} {\stackrel{slope}{\cfrac{15}{8}} ~\hfill \stackrel{reciprocal}{\cfrac{8}{15}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{8}{15}}}`

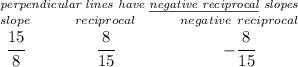
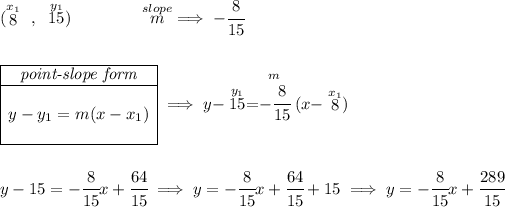
so we're really looking for the equation of a line with a slope of -8/15 and that passes through (8 , 15).

`(\stackrel{x_1}{8}~,~\stackrel{y_1}{15})\qquad\qquad \stackrel{slope}{m}\implies -\cfrac{8}{15} \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{15}=\stackrel{m}{-\cfrac{8}{15}}(x-\stackrel{x_1}{8}) \\\\\\ y-15=-\cfrac{8}{15}x+\cfrac{64}{15}\implies y=-\cfrac{8}{15}x+\cfrac{64}{15}+15\implies y=-\cfrac{8}{15}x+\cfrac{289}{15}`

Answer 2

We are given two points (0,0) and (8,15)

15-0/8-0= 15/8 --> 8/15 for tangent

y=8/15(x) + b

plug in point A

y= 8/15 (x) +3.6