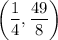Question

Given: f(x) = -2x² +x+6
5.1 Calculate the coordinates of the turning point of f.​

Answer 1

answers

f=1/4=49/8

Explanation:

identify the coefficients

a=-2, b=1

substitute the coefficient into the expression

x= -1/((2x(-2))

then solve it out the equation

x=1/4

evaluate the function x =1/4

f(x) =-2x²+x+6(1/4)

f=1/4=49/8

Answer 2

`\left((1)/(4),(49)/(8)\right)`

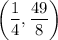
Explanation:

Turning points (stationary points) occur when the gradient of a graph is zero.

To find when the gradient of the graph is zero, differentiate the function, set it zero, then solve for x.

Given function:

`f(x)=-2x^2+x+6`

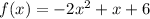
Differentiate:

`\implies f'(x)=(2)(-2)x^(2-1)+(1)x^(1-1)+6(0)`

`\implies f'(x)=-4x+1`

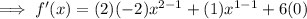
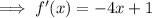
Set the differentiated function to zero and solve for x:

`\implies f'(x)=0`

`\implies -4x+1=0`

`\implies 4x=1`

`\implies x=(1)/(4)`

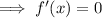
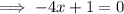
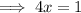
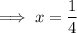
To find the y-coordinate, input the found value of y into the given function:

`\implies f\left((1)/(4)\right)=-2\left((1)/(4)\right)^2+\left((1)/(4)\right)+6`

`\implies f\left((1)/(4)\right)=(49)/(8)`

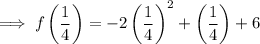
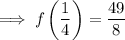
Therefore, the turning point of the function is:

`\left((1)/(4),(49)/(8)\right)`