Answer:

Explanation:
Turning points (stationary points) occur when the gradient of a graph is zero.
To find when the gradient of the graph is zero, differentiate the function, set it zero, then solve for x.
Given function:
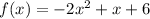
Differentiate:
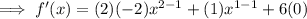

Set the differentiated function to zero and solve for x:
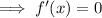

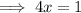
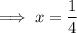
To find the y-coordinate, input the found value of y into the given function:
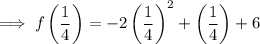
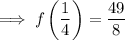
Therefore, the turning point of the function is:
