Question

Circle O is centered on the origin with a diameter of 14 units. Determine if the point (−3,2√10) is on the circle. Explain your reasoning.

Answer 1

Determine the equation of the circle.

Equation of a circle

`(x-a)^2+(y-b)^2=r^2`

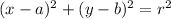
(where (a, b) is the center and r is the radius)

Given:

• center = (0, 0)
• diameter = 14
  ⇒ radius = 14 ÷ 2 = 7

Substitute the given values into the formula to determine the equation of the circle:

`\implies (x-0)^2+(y-0)^2=7^2`

`\implies x^2+y^2=49`

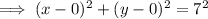
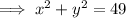
Given point:
`(-3,2√(10))`

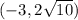
Input the x and y values of the given point into the derived circle equation. If it equals 49, then the point is on the circle:

`\implies (-3)^2+(2 √(10))^2=9+40=49`

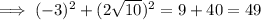
Therefore, the given point is on the circle centered at the origin with a diameter of 14 units.