Answer:
Determine the equation of the circle.
Equation of a circle

(where (a, b) is the center and r is the radius)
Given:
- center = (0, 0)
- diameter = 14
⇒ radius = 14 ÷ 2 = 7
Substitute the given values into the formula to determine the equation of the circle:
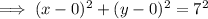
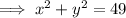
Given point:
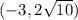
Input the x and y values of the given point into the derived circle equation. If it equals 49, then the point is on the circle:
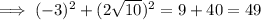
Therefore, the given point is on the circle centered at the origin with a diameter of 14 units.