Answer:
The sample must be greater than 55
Explanation:
Confidence = 99% = 0.99
α = 1 - C = 1 - 0.99 = 0.01
α/2 = 0.01/2 = 0.005
The z score of α/2 (0.005) corresponds to the z score of 0.495 (0.5 - 0.005) which is equal to 2.576
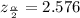
The margin of error (E) is given by the formula:

n > 55
The sample must be greater than 55 so that the margin of error will not exceed 35 hours