Question

If a 20-kg object dropped in air has a terminal speed of 60 m/s, what was its acceleration at 30 m/s

Answer 1

a = 7.35 m/s²

Step-by-step explanation:

Given that,

Mass of a object, m = 20 kg

The terminal speed of the object,
`v_t=60\ m/s`

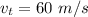
We need to find its acceleration at 30 m/s.

It is a case on Newton's second law of motion. Its mathematical form can be given by :

`mg-F_D=ma`

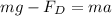
Here,
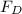`F_D` is the Drag force,
`F_D=kv_t^2`

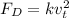
Putting all the values,

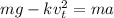`mg-kv_t^2=ma` ....(1)

Here, a = 0 Firstly we find the value of k (constant)

`k=(mg)/(v_t^2)\\\\k=(20* 9.8)/(60^2)\\\\k=0.0545`

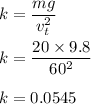
Now, put the value of k in equation (1) and here put v = 30 m/s

`a=(mg-kv_t)/(m)\\\\a=(20(9.8)-0.0544* 30^2)/(20)\\\\a=7.35\ m/s^2`

So, its acceleration at 30 m/s is 7.35 m/s².