Answer:
The magnetic field at the center of a circular current loop of radius R divided by the magnetic field at a distance R away from a very long straight wire carrying the same current value I is
 or 3.14
or 3.14
Step-by-step explanation:
The magnetic field at center of a circular loop is given by

Where B is the magnetic field
 is the free space permeability constant (
is the free space permeability constant (
 = 4π × 10⁻⁷ N/A²)
= 4π × 10⁻⁷ N/A²)
 is the current
is the current
and
 is the radius
is the radius
For the magnetic field of a long straight wire, it is given by

Where B is the magnetic field
 is the free space permeability constant (
is the free space permeability constant (
 = 4π × 10⁻⁷ N/A²)
= 4π × 10⁻⁷ N/A²)
 is the current
is the current
and
 is the distance from the wire
is the distance from the wire
Then, to calculate the magnetic field at the center of a circular current loop of radius R divided by the magnetic field at a distance R away from a very long straight wire carrying the same current value I, that will be

=
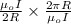
=

(NOTE:
 = 3.14)
= 3.14)
Hence, the magnetic field at the center of a circular current loop of radius R divided by the magnetic field at a distance R away from a very long straight wire carrying the same current value I is
 or 3.14.
or 3.14.