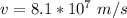Answer:
The speed is
Step-by-step explanation:
From the question we are told that
The real wavelength is
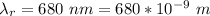
The observed wavelength is
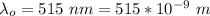
Generally the real wavelength of the stop light according to doppler effect is mathematically as

Here c is the speed of the light
and v is the speed of the physicist
So
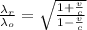
=>

=>
![[(680nm)/(515nm) ]^2= (1 + (v)/(c) )/(1 - (v)/(c) )](https://img.qammunity.org/2021/formulas/physics/college/za37zr8tddkqt644ple5wno35ahg05h3cm.png)
=>
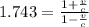
=>
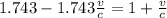
=>

=>
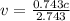
=>
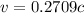
substituting
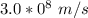 for c
for c
=>
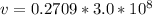
=>