Question

The volume of a rectangular box with a square base remains constant at 1000 cm3 as the area of the base increases at a rate of 4 cm2 /sec. Find the rate at which the height of the box is decreasing when each side of the base is 12 cm long.

Answer 1

The rate at which the height of the box is decreasing when each side of the base is 12 centimeters long is 0.193 centimeters per second.

Explanation:

We can represent the volume of the rectangular box with a square base (
`V`), measured in cubic centimeters, by means of this formula:

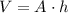`V = A\cdot h` (Eq. 1)

Where:

`A` - Area of the base of the box, measured in centimeters.

`h` - Height of the rectangular box, measured in centimeters.

Given that volume remains constant, we clear the height of the box as follows:

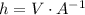`h = V\cdot A^(-1)` (Eq. 1b)

By Differential Calculus, we get the expression for the rate of change of the height:

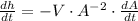`(dh)/(dt) = - V\cdot A^(-2)\cdot (dA)/(dt)` (Eq. 2)

Where:

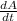`(dA)/(dt)` - Rate of change of the area of the base in time, measured in square centimeters per second.

`(dh)/(dt)` - Rate of change of the height of the box in time, measured in centimeters per second.

If we know that
`V = 1000\,cm^(3)`,
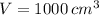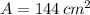`A = 144\,cm^(2)` and
`(dA)/(dt) = 4\,(cm^(2))/(s)`, then the rate of change of the area of the base in time is:

`(dh)/(dt) = -(1000\,cm^(3))\cdot (144\,cm^(2))^(-2) \cdot \left(4\,(cm^(2))/(s) \right)`

`(dh)/(dt) = -0.193\,(cm)/(s)`

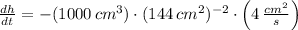
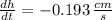
The rate at which the height of the box is decreasing when each side of the base is 12 centimeters long is 0.193 centimeters per second.