Question

Calculate the wavelength, in meters, associated with a g golf ball moving at 20. m/s (about 45 mph).

Answer 1

The wavelength of a moving golf ball can be calculated using the de Broglie hypothesis with the formula λ = h / mv. Given a mass of 0.045 kg and a velocity of 20 m/s, the calculated wavelength is approximately
`7.39 x 10^(-34 m).`Step-by-step explanation:

To calculate the wavelength of a moving golf ball, we apply the de Broglie hypothesis which states that any moving particle has an associated wave character. The formula to calculate the wavelength λ is given by λ = h / mv, where h is Planck's constant (
`6.626 x*10^(-34 m)2 kg / s`m is the mass of the particle, and v is its velocity.

Assuming a golf ball has a mass of 0.045 kg (45 g) and a velocity of 20 m/s, we substitute these values into the formula to get λ = 6.626 x 10-34 / (0.045 kg × 20 m/s). Calculating this gives a wavelength of approximately
`7.39 * 10^{-34 m` ball.

Answer 2

Complete Question

Calculate the wavelength, in meters, associated with a 56g golf ball moving at 20. m/s (about 45 mph).

Answer:

The value is
`\lambda = 5.92 *10^(-34) \ m`

Step-by-step explanation:

From the question we are told that

The speed of the golf ball is
`v = 20 \ m/s`

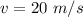
The mass is
`m = 56 \ g = 0.056 \ kg`

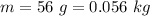
Generally from Broglie's equation we have that

`\lambda = (h)/(mv )`

Here h is the Planck constant with value

`h = 6.626 *10^(-34) \ kg\cdot m^2\cdot s^(-1)`

Here
`\lambda` is the wavelength associated with the golf ball

So

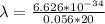
`\lambda = (6.626 *10^(-34))/( 0.056 * 20)`

=>
`\lambda = 5.92 *10^(-34) \ m`