Answer:
The last option is correct: -4.3%
Explanation:
Continuous Exponential Growth or Decay
The exponential e is used when modeling continuous growth or decay that occurs naturally such as populations, bacteria, radioactive decay, etc.
If a quantity grows or decays continuously by a fixed percent, the pattern can be described by the function:

Where P(t) is the value at the time t
k is the continuous growth/decay rate. If positive is for growth if negative is for decay.
The given function is:
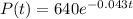
It can be seen the value of k is:
k = -0.043
Or, expressed as a percentage:
k = -4.3%
The last option is correct: -4.3%