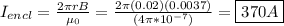Hi there!
We can use Ampère's Law to derive an expression for the magnetic field strength produced by an infinitely long current-carrying wire:
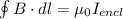
B = Magnetic Field Strength (T)
dl = Differential length along path
μ₀ = Permeability of Free Space (Tm/A)
I = Enclosed current (A)
The integral is a cross product, so the cosine of the angle between the magnetic field and the path of integration is used. However, for a straight current-carrying wire, the path is ALWAYS parallel to the magnetic field, so since cos(180) = 1, we can disregard the cross product.
Additionally, the path of integration is equivalent to:
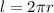
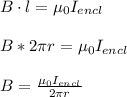
Rearrange to solve for enclosed current: