Answer:
The length of QR is 29.9 cm
Explanation:
Let us revise the sine and cosine rules
In triangle ABC:
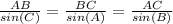 ⇒ sine rule
⇒ sine rule
(AC)² = (AB)² + (BC)² - 2(AB)(BC)cos(∠B) ⇒ cosine rule
Let us use these rules to solve the question
In Δ PQS
∵

∵ PS = 11.7 cm
∵ m∠P = 95°, m∠Q = 28°
→ Substitute them in the rule above
∴
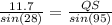
→ By using cross multiplication
∴ QS × sin(28) = 11.7 × sin(95)
→ Divide both sides by sin(28) to find QS
∴ QS = 24.82680292 cm
Now let us use the cosine rule to find QR
In Δ QSR
∵ (QR)² = (QS)² + (RS)² - 2(QS)(RS)cos(∠QSR)
∵ RS = 10.2 cm
∵ m∠QSR = 110°
→ Substitute these values in the rule above
∴ (QR)² = (24.82680292)² + (10.2)² - 2(24.82680292)(10.2)cos(110)
∴ (QR)² = 893.631984
→ Take √ for both sides
∴ QR = 29.89367799
→ Round it to 3 significant figures
∴ QR = 29.9 cm