Answer:
6.18 ft
Explanation:
The ramp forms a right triangle.
We know two of the lengths of the right triangle, therefore, we would apply pythagorean theorem to find the longest length of the triangle, which is the length of the ramp.
The given lengths are 1.5 ft and 6 ft. The length of the ramp is the length of the longest side (hypotenuse length).
Thus, applying pythagorean theorem:
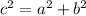 , where,
, where,
a = 1.5 ft
b = 6 ft
c = length of ramp
Substituting the values:
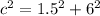
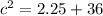
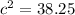
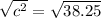
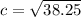
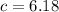 (nearest hundredth)
(nearest hundredth)
length of the ramp = 6.18 ft