Answer:
b. 433 N
Step-by-step explanation:
From Newton's law of universal gravitation,
F =
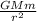 ........... 1
........... 1
where: F is the force of attraction, G is Newton's universal gravitation constant, M is the mass of massive object, m is the mass of the other object and r is the radius.
Also, from Newton's second law,
F = mg ............ 2
Thus,
mg =
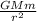
g =
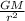 ................ 3
................ 3
Equation 3 can be used to determine the gravitational force on Titan.
Given that: G = 6.6743 x
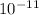
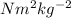 , M (mass of Titan) = 1.35 x 10^23 kg, and
, M (mass of Titan) = 1.35 x 10^23 kg, and
r =
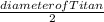
=
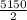
= 2575 km
r = 2575 000 m
g =
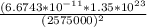
=
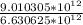
= 1.3589
g = 1.36 m/
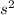
The acceleration due to gravity, g, on Titan's surface is 1.36 m/
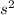 .
.
On the earth,
weight = mass x acceleration due to gravity
3120 = m x 9.81
m =
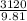
= 318.0428135
The mass of the probe is 318 kg.
So that its weight on the surface of Titan = m x g
= 318 x 1.36
= 432.5 N
The weight of the probe on the surface of Titan is 433 N.