Answer:
i) 23.9 Ib ( lift )
ii) 0.25 Ib ( drag )
iii) -2.68 ft. Ib ( moment about )
Step-by-step explanation:
Given data:
Angle of attack of wing = 5°
airflow velocity = 100 ft/s
NACA 1412 airfoil section
i) calculate The lift
L =
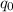

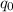 = dynamic pressure = 11.9 Ib/ft^2 ( as calculated using
= dynamic pressure = 11.9 Ib/ft^2 ( as calculated using
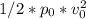 )
)
s = area = ( 1ft ) ( c ) = ( 1 ) ( 3 ) = 3ft^2
 = lift coefficient = 0.67 ( refer to appendix D at an angle of 5° )
= lift coefficient = 0.67 ( refer to appendix D at an angle of 5° )
Hence the lift ( L) = 11.9 * 3 * 0.67 = 23.9 Ib
ii) calculate The drag
D =
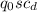
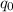 = 11.9 Ib/ft^2
= 11.9 Ib/ft^2
s = 3ft^2
Cd ( drag coefficient ) = 0.007
hence drag ( D ) = 11.9 * 3 * 0.007 = 0.25 Ib
iii) calculate Moment about
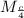 =
=
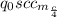
qo = 11.9
s = 3 ft^2
c = 3 ft
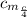 = - 0.025
= - 0.025
hence moment about = ( 11.9 * 3 * 3 * - 0.025 ) = -2.68 ft. Ib