Answer:
2.5 inches
Explanation:
The general form of the equation of a circle is
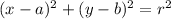
Where
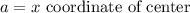

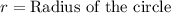
If the circle's center is on the origin the equation becomes
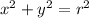
Here the equation is of the form
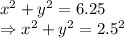
So, the radius of the circle is 2.5 inches.
Hence the miniature golf holes are 2.5 inches wide.