9514 1404 393
Answer:
see below
Explanation:
Step 1: count the number of decimal places in each number. 4.58 has 2; 0.025 has 3. The total number of decimal places is 2+3=5. (It may be useful to count, then drop, any trailing zeros to the right of the decimal point. These will be appended to the final answer at the end. 0.2500 → 0.25, for example, and 2 trailing 0s would be added to the final result.)
Step 2: write the numbers one below the other, aligning the digits into columns starting from the least significant digit. It can be useful to place the number with the smallest number of significant digits on the bottom. The top number is called the multiplicand; the bottom number is called the multiplier. (see the 2nd attachment for more vocabulary)
Step 3: Working right to left, starting with the least significant digits, multiply the multiplier digit by each of the multiplicand digits in turn. Write down the least-significant digit of the first product in the column below the digit of the multiplier you're using. Any 10s digit in the product is carried into the next column.
Here, the first product is 5×8 = 40, so the 0 (ones digit of 40) is written under the 5 as the least-significant digit of the first partial product. The 4 (tens digit of 40) is carried to the next column to the left. The number written in that column of the first partial product is the ones digit of the sum of 5×5 and 4. That sum is 29, so 9 is written to the left of the 0, and 2 is carried to the next column. Finally, the result of 5×4+2 = 22 is written in the two partial product columns left of the 9 and 0 previously written.
Alternate method of writing partial products. I sometimes find it too tedious to deal with the carries from each of the product/sums, so I use two rows to write each partial product. I use one row for the ones digits of the product, and another for the tens digits. Instead of one partial product row of 2290, this would be ...
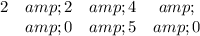
This is a personal adaptation of the method being described here. You can see that the sums of the columns still add to 2290.
__
Step 4: Repeat the process for each multiplier digit, working left to right. Again, the least-significant digit of the first multiplication result is aligned under the multiplier digit. This maintains its correct place value in the result.
Step 5: Add the partial products, carrying as required.
Step 6: Place the decimal point, counting digits from the right end of the product. If necessary, add leading zeros to the product. The total number of product decimal places is the total number of decimal places in the numbers being multiplied. (If any trailing zeros were discarded at the beginning, add those after the decimal point is placed. That is, the final total number of decimal digits should be the sum of the numbers of decimal digits in the original multiplier and multiplicand. 0.3×0.100, for example will have a product of 0.0300: .3×.1 ⇒ .03, then the two trailing zeros from 0.100 are added back on for a total of 4 decimal digits.
_____
Additional comments
This gets you the exact product of the two numbers. Often, that product will need to be modified to fit the problem that required it. For example, it may need to be rounded, or its number of significant digits adjusted.
Sometimes, it is easier to do the multiplication with the numbers written in scientific notation.