Question

2. The coordinates of the vertices of ΔARC are A(3,3), R(1,-1), and C(-2,1). Angela is trying to determine whether this shape is a right triangle or not. She has made a mistake in the work below the graph. Explain the mistake and show the correct solution.

Angela’s solution:

slope of AR = (3-(-1))/(3-1)=3/2

slope of RC = (1-(-1))/(-2-1)=2/(-3)=-2/3

slope of AC = (3-1)/(3-(-2))=2/5

Since AR and RC are opposite reciprocal slopes, those two sides are perpendicular, and the triangle is a right triangle.

Answer 1

the mistake in the slope is , (3 - (-1)/(3 -1) = 4/2 ≠ 3/2

Explanation:

Answer 2

Her mistake was in the slope for segment AR, (3 - (-1)/(3 -1) = 4/2 ≠ 3/2

Explanation:

The steps for obtaining the slope is given as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

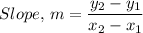
Where;

(x₁, y₁) and (x₂, y₂) are the coordinates of the endpoints of the line

The coordinates of the vertices are;

A(3, 3), R(1, -1), and C(-2, 1)

Slope of AR = (3 - (-1))/(3 - 1) = (3 + 1)/(3 - 1) = 4/2 = 2

The slope of RC = (-1 - 1)/(1 - (-2)) = -2/(1 + 2) = -2/3

The slope of AC = (3 - 1)/(3 - (-2)) = 2/(3 + 2) = 2/5

Therefore, her mistake was the value of the double negation in the numerator when finding the slope of AR is 4 rather than 3