Answer:
The correct answer is option (A) 8π cm; 16π cm².
Solution :
Finding the circumference of circle by substituting the values in the formula :

 C = Circumference
C = Circumference
 π = 3.14 or 22/7
π = 3.14 or 22/7
 r = radius
r = radius
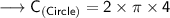
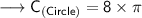
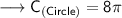
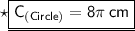
Hence, the circumference of circle is 8π cm.

Finding the area of circle by substituting the values in the formula :

 A = Area
A = Area
 π = 3.14 or 22/7
π = 3.14 or 22/7
 r = radius
r = radius
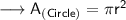
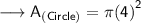
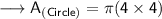
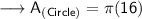
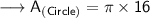

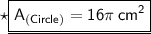
Hence, the area of circle is 16π cm².
