Answer:
The slope of the secant line joining (2, 0) and (8, 48) is 8.
Explanation:
Let
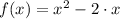 , from Analytical Geometry we remember that slope of a secant line is defined by:
, from Analytical Geometry we remember that slope of a secant line is defined by:
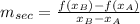 (Eq. 1)
(Eq. 1)
Where:
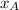 ,
,
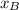 - Initial and final independent variables, dimensionless.
- Initial and final independent variables, dimensionless.
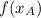 ,
,
 - Initial and final dependent variables, dimensionless.
- Initial and final dependent variables, dimensionless.
Now we proceed to find the values of each dependent variable:
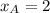
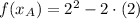
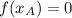
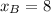
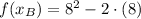
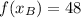
And slope of the secant slope is determined after replacing every variable:
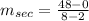
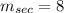
The slope of the secant line joining (2, 0) and (8, 48) is 8.