Question

At noon, ship A is 50 nautical miles due west of ship B. Ship A is sailing west at 16 knots and ship B is sailing north at 15 knots. How fast (in knots) is the distance between the ships changing at 5 PM

Answer 1

The distance between the ships changing at 5 PM is 21.355 knots

Explanation:

let x = distance traveled by ship A

y = distance traveled by ship B

Let z be the distance between Ship A and Ship B

Ship A is sailing west at 16 knots and ship B is sailing north at 15 knots.

Refer the attached figure

x=50+16t

y = 15t

At 5 Pm

x=50+16(5)=130

y = 15(5)=75

We will use Pythagoras theorem

`z^2=x^2+y^2`

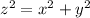
At 7 pm
`z = √((130)^2+(75)^2)=150.08`

`z^2=(50+16t)^2+(15t)^2`

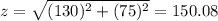
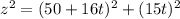
Differentiating both sides

`2z (dz)/(dt)=2(50+16t)(16)+2(15t)(15)\\ (dz)/(dt)=((50+16t)(16)+(15t)(15))/(z)\\ (dz)/(dt)=((50+16(5))(16)+(15(5))(15))/(150.08)\\ (dz)/(dt)=21.355`

Hence The distance between the ships changing at 5 PM is 21.355 knots