Answer:
33.1144 °C
Step-by-step explanation:
From the information given;
The first step is to find the mean temperature
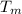 by using the formula:
by using the formula:
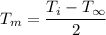
where:
 = initial temperature = 40 °C
= initial temperature = 40 °C
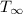 = ambient temperature = 10 °C
= ambient temperature = 10 °C
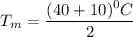

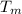 = 25 °C
= 25 °C
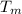 = (25 + 273) K
= (25 + 273) K
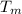 = 298 K ≅ 300 K
= 298 K ≅ 300 K
The following properties expressed below were obtained from the thermal physical properties table.
For soda-lime glass at the temperature of 300 K:
Density
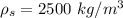
Thermal conductivity
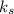 = 1.4 W/m.K
= 1.4 W/m.K
Specific heat
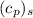 = 750 J/kg.K
= 750 J/kg.K
For bakelite at the temperature of 300 K:
Density
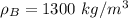
Thermal conductivity
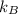 = 1.4 W/m.K
= 1.4 W/m.K
Specific heat
 = 1465 J/kg.K
= 1465 J/kg.K
From these data; The next process is to find out the thermal diffusivity of each component.
To start with soda-lime glass by using the expression:

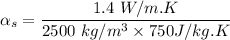
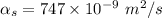
For Bakelite: The thermal diffusivity is computed as:
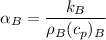

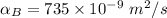
From the above two results, we will realize that
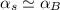
Thus, as obvious as it is; we presume that the uniform thermal diffusivity
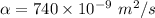
However, the diameter of the sphere can be estimated by the summation of the diameter of the glass sphere
 with twice the thickness of the sphere (L)
with twice the thickness of the sphere (L)
i.e.

D = 25 mm + 2 (10 mm)
D = 45 mm

D = 45 × 10⁻³ m
The expression for Biot Number can be estimated by using the formula:

Given that:
h = 30 W/m².k
D = 45 × 10⁻³ m
k = 1.4 W/m.K
Similarly, to estimate the Fourier No
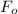 by using the expression:
by using the expression:
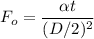
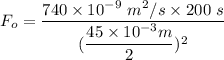
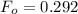
It is obvious that
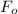 is > 0.2, thus, the validity of one term approximation is certain.
is > 0.2, thus, the validity of one term approximation is certain.
Again; the Biot Number is calculated by using the formula:
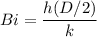

Bi = 0.482
Bi
 0.5
0.5
We obtain the Eigen coefficient
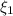 as well as the coefficient for a sphere
as well as the coefficient for a sphere
 using the Bi Number:
using the Bi Number:
From one-term approximation of transient 1 heat conduction in the sphere;

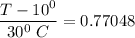

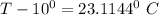
T = (23.1144 + 10) °C
T = 33.1144 °C