Answer:
D) (-1.6, -2.5)
Explanation:
Please see attached for the graphing of the two functions.
The solution is the point where the two curves intersect.
From inspection of the graph, the solution is (-1.6, -2.5)
Proof
Given functions:
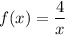
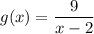
To find the solution:
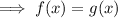

Cross multiply:
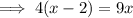
Expand:

Simplify:

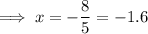
Inputting the found value of x into one of the equations and solving for y:
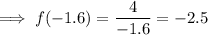
Therefore, the solution to f(x) = g(x) is (-1.6, -2.5) thus proving the graphed solution.