Question

PLEASE I NEED THIS ASAP (PLEASE DON'T DO IT FOR POINTS I REALLY NEED IT).

Answer 1

Used graphing calculator=Desmos

• f(x)=4/x
• g(x)=9/x-2

Graph attached

for f(x)=g(x)

Solution is

• (-1.6,-2.5)

Answer 2

D) (-1.6, -2.5)

Explanation:

Please see attached for the graphing of the two functions.

The solution is the point where the two curves intersect.

From inspection of the graph, the solution is (-1.6, -2.5)

Proof

Given functions:

`f(x)=(4)/(x)`

`g(x)=(9)/(x-2)`

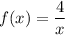
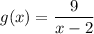
To find the solution:

`\implies f(x)=g(x)`

`\implies (4)/(x)=(9)/(x-2)`

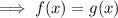
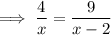
Cross multiply:

`\implies 4(x-2)=9x`

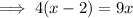
Expand:

`\implies 4x-8=9x`

Simplify:

`\implies -5x=8`

`\implies x=-(8)/(5)=-1.6`

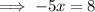
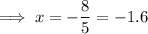
Inputting the found value of x into one of the equations and solving for y:

`\implies f(-1.6)=(4)/(-1.6)=-2.5`

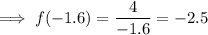
Therefore, the solution to f(x) = g(x) is (-1.6, -2.5) thus proving the graphed solution.