Question

)If a force of 5.00 N is needed to open a 90.0 cm wide door when applied at the edge opposite the hinges, what force must be applied to open the door if you push against the door 35.0 cm from the hinged side

Answer 1

A force of 12.857 newtons must be applied to open the door.

Step-by-step explanation:

In this case, a force is exerted on the door, a moment is performed and the door is opened. If moment remains constant, the force is inversely proportional to distance respect to axis of rotation passing through hinges. That is:

`F \propto (1)/(r)`

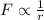
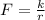`F = (k)/(r)` (Eq. 1)

Where:

`F` - Force, measured in newtons.

`k` - Proportionality ratio, measured in newton-meters.

`r` - Distance respect to axis of rotation passing through hinges, measured in meters.

From (Eq. 1) we get the following relationship and clear the final force within:

`F_(A)\cdot r_(A) = F_(B)\cdot r_(B)`

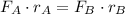
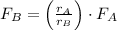`F_(B)=\left((r_(A))/(r_(B)) \right)\cdot F_(A)`(Eq. 2)

Where:

`F_(A)`,
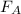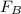`F_(B)` - Initial and final forces, measured in newtons.

`r_(A)`,
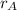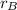`r_(B)` - Initial and final distances, measured in meters.

If we know that
`F_(A) = 5\,N`,
`r_(A) = 0.9\,m` and
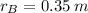`r_(B) = 0.35\,m`, then final force is:

`F_(B)= \left((0.9\,m)/(0.35\,m) \right)\cdot (5\,N)`

`F_(B) = 12.857\,N`

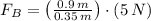
A force of 12.857 newtons must be applied to open the door.